A math problem: enriching uranium!
The uranium enriching process is a simple yet hard process. We want to reach 3.5% uranium and we only have got 0.7% uranium. To achieve this goal, we should feed the uranium to a centrifuge. For each 2 units of x% uranium which we feeds to the centrifuge, we gets 1 unit of (x-0.1)% and 1 unit of (x+0.1)% uranium. For example a unit of 0.6% and a unit of 0.8% for 2 units of 0.7%. 0.0% uranium will be discarded. Units are always positive integer and we cannot feed 1 unit of uranium, like to get two $ \frac{1}{2} $ unit.
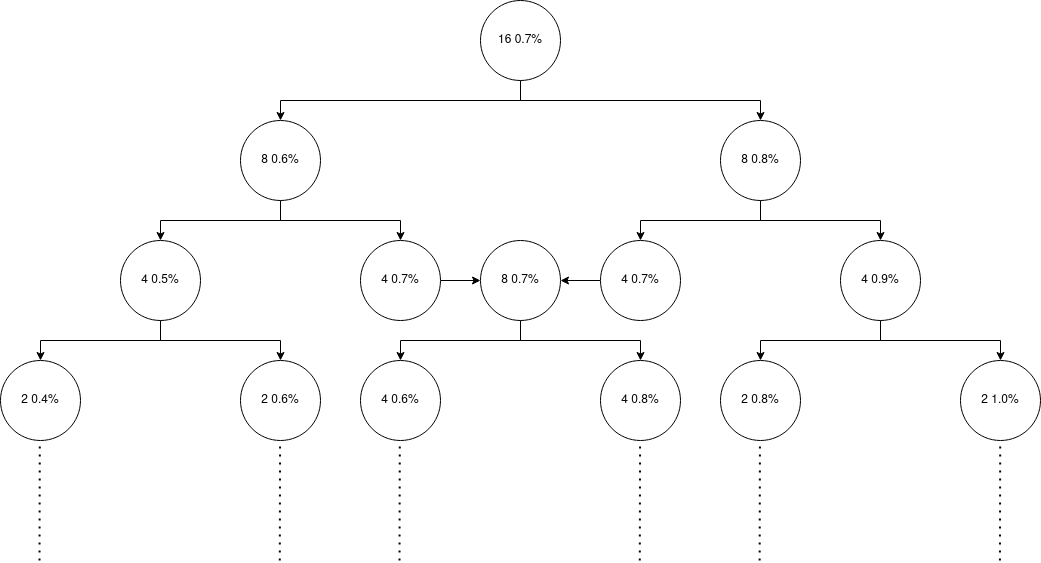
So to reach 3.5% uranium, 3 questions get raised:
Will we be able to produce 3.5% uranium from $m$ units of 0.7% uranium?
For $m$ units of 0.7% uranium how many units of 3.5% uranium can we produce?
If with some units of 0.7% uranium, we cannot produce at least a unit of 3.5% uranium, what is the richest which we can produce?
You can solve these questions either by your math skills or your coding skills. Good luck :)
